사용자 기반 이웃 모델
{유사도 함수, 예측 함수, 피어그룹 필터링, 롱테일 영향 고려한 피어슨 계수}의 변형
1. 유사도 함수 변형
동시에 평점 매겨진 아이템 수(Iu, Iv 교집합)가 적을 때, sim(u,v) 대신 discountedSim(u,v)를 사용함.
+ beta : 중복되어야 하는 평균적인 아이템 수 (공통으로 평점 매긴)
+ beta에 비해 공통아이템 수가 적다면, 유사도를 평가하기에 신뢰도가 낮기 때문에 아래와 같은 과정으로 변환함.

예시)
beta=5, 공통아이템 =1이라면
디스카운트 텀이 min(1,5)/5 = 1/5가 되고, sim(u,v)에 곱해져 전체 유사도 값을 의도적으로 낮춤.
+ 그 외 공통 아이템이 beta보다 크다면 (>=5), 디스카운트 텀이 min(5,5)/5 = 1이 되어 기존의 sin(u,v)와 같아짐.
=> 아이템 수가 적을 때만 자동적으로 값이 낮아짐.
2. 예측 함수 변형
Mean-Centering 대신 Z-score 활용.
평균 중심화는 단순히 중심만 0으로 맞추는데, 사용자마다의 평점 분포가 다를 수 있기 때문에 분포의 폭도 보정해야 함.
? 사용자마다의 평점 분포가 다르다 ?
- 어떤 사람은 5~10점, 어떤 사람은 0~6점 안에서만 평점을 매김.
⇒ 단순 mean-centering만 해서는 상대적 강도가 반영되지 않음.
1. 표준편차 계산
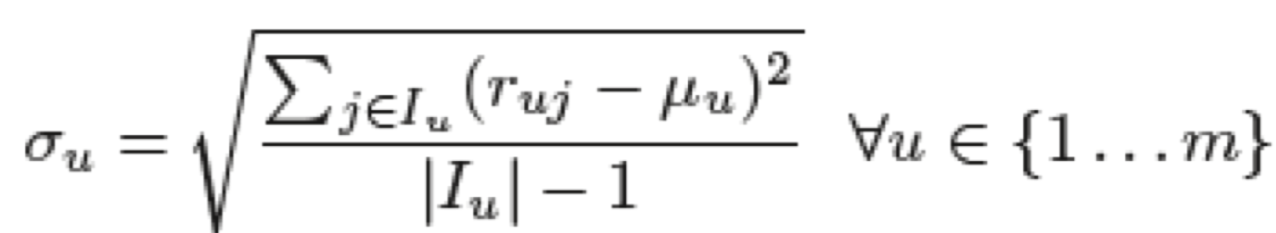
2. 표준화된 평점 계산 (z-score)

각 data가 평균으로부터 얼만큼의 표준편차만큼 떨어져있는지를 나타냄.
z-score는 평균을 0, 분산을 1로 변환하여, normalization 효과에 아이템 평점의 분산 정도도 가미함.

* 분산(표준편차)은 Data가 많다는 전제 하에 고려한다. Data가 적을 때도 고려하면 값이 튈 수 있음.
3. Z-score 이용한 평점 예측 계산
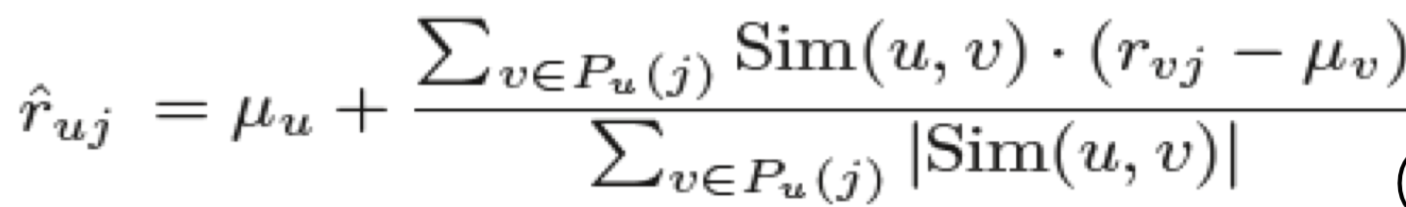

3. 피어그룹 필터링 변형
1. 피어슨 상관 계수 값을 내림차순 정렬 후, top-k 그룹을 설정.
2. top-k 내에서 음의 상관계수를 갖는 비교대상 제외 (혹은 임의의 임계값보다 작은 것)


예시로, k=3으로 설정하면 user 5도 비교대상이 됨.
그러나 -0.87은 반대의 경향이 크기 때문에 악영향을 끼치므로 대상에서 제외시킴.
4. 롱테일 영향을 고려한 피어슨 계수 변형
많이 평가된 아이템의 영향은 줄이고, 드물게 평가된 아이템의 가중치는 높인다는 아이디어.
[롱테일 문제]
- 어떤 아이템(예: 인기 드라마)은 거의 모든 사용자가 평가함
- 이런 아이템은 모든 사용자에게 공통된 정보라서 유사도 계산에 도움이 되지 않음
- 반대로, 비주류 아이템(롱테일)은 취향의 특이성을 드러냄
[해결 방법]
문서 검색의 IDF (Inverse Document Frequency) 차용
- m: 전체 사용자 수
- m_: 아이템 j를 평가한 사용자 수
→ 사용자 수가 적을수록 가중치가 증가함. (희소성 있는 아이템 가중치 up)


로그 그래프는 처음에 확 커지다가 점점 폭이 줄어드는 형태임. -> 가중치를 적당히 키우겠다는 뜻.
'추천시스템' 카테고리의 다른 글
| [추천시스템] week3 - 아이템 기반 이웃 모델 (평점 예측, 복잡도) (0) | 2025.04.13 |
|---|---|
| [추천시스템] week2 - 사용자 기반 이웃 모델 (평점 예측 과정) (2) | 2025.04.13 |